El diseño óptimo de un sistema de vapor dependerá en gran medida de si la tasa de consumo de vapor se ha calculado con precisión. Esto permitirá calcular el tamaño de las tuberías y dimensionar los equipos auxiliares como válvulas de control y purgadores de vapor para que proporcionen los mejores resultados posibles. Se puede calcular la demanda de vapor de la planta utilizando diferentes métodos:
- Cálculo – Mediante el análisis de la salida de calor en un elemento de la planta usando las ecuaciones de transferencia de calor, se puede obtener una estimación para el consumo de vapor. Aunque la transferencia de calor no es una ciencia exacta y puede haber muchas variables desconocidas, se pueden utilizar datos experimentales anteriores de aplicaciones similares. Los resultados conseguidos con este método suelen ser lo suficientemente precisos para la mayoría de los propósitos.
- Medición – Se puede determinar el consumo de vapor por medición directa, usando equipos de medición de caudal. Estos proporcionan datos relativamente precisos sobre el consumo de vapor de una planta existente.Sin embargo, para una planta que se encuentra todavía en la etapa de diseño, o que no está en funcionamiento, este método es de poca utilidad.
- Potencia térmica – La potencia térmica (design rating) aparece a menudo en la placa de características de un equipo individual de una planta, según lo dispuesto por el fabricante. Normalmente indica la potencia calorífica prevista en kW, pero el consumo de vapor requerido en kg/h dependerá de la presión de vapor recomendada.
Cualquier cambio en un parámetro puede alterar la potencia calorífica prevista, significa que la potencia térmica (diseño) y la carga conectada (consumo real de vapor) no será la misma. El valor dado por el fabricante es una indicación de la capacidad ideal de un equipo y no necesariamente corresponde a la carga conectada.
Cálculo del consumo del vapor industrial
En la mayoría de los casos, se requiere que el calor en el vapor haga dos cosas:
- Producir un cambio en la temperatura del producto, proporcionando un ‘componente de calentamiento’.
- Mantener la temperatura del producto según se vaya perdiendo el calor por causas naturales o por el diseño, proporcionando un componente de ‘pérdida de calor’.
En cualquier proceso de calentamiento, el ‘componente de calentamiento’ disminuirá a medida que se eleve la temperatura del producto y se reduce el diferencial de temperatura entre el serpentín de calentamiento y el producto. Sin embargo, el componente de pérdida de calor aumentará a medida que la temperatura del producto suba y se pierda más calor con el medio ambiente desde el recipiente o tubería.
La demanda total de calor en cualquier momento es la suma de estos dos componentes.
La ecuación utilizada para establecer la cantidad de calor necesaria para elevar la temperatura de una sustancia, se puede desarrollar para que se aplique a una amplia gama de procesos de transferencia de calor.
Donde:
Q = Cantidad de energía (kJ)
m = Masa de la sustancia (kg)
cp = Calor específico de la sustancia (kJ/kg °C)
△T = Salto de temperatura de la sustancia (°C)
En su forma original, esta ecuación se puede usar para determinar la cantidad total de energía calorífica en todo el proceso. Sin embargo, en su forma actual, no tiene en cuenta la tasa de transferencia de calor. Para establecer las tasas de transferencia de calor, los diferentes tipos de aplicación de intercambio de calor se pueden dividir en dos amplias categorías:
- Aplicaciones estáticas – en el que el producto que se está calentando es una masa fija y un único lote dentro de los confines de un recipiente.
- Aplicaciones dinámicas – en donde un fluido calentado fluye constantemente sobre la superficie de transferencia de calor.
Aplicaciones estáticas para calcular consumo de vapor
En aplicaciones estáticas, el fluido de proceso se mantiene como un único lote dentro de un recipiente. Un serpentín de vapor situado en el recipiente, o una camisa de vapor alrededor del recipiente, constituyen la superficie de calentamiento. Ejemplos típicos incluyen acumuladores para almacenamiento de agua caliente y tanques de almacenamiento de petróleo, donde un gran tanque de acero circular se llena con petróleo viscoso que requiere calor antes de que pueda ser bombeado.
Algunos procesos tienen que ver con calentarsólidos; ejemplos típicos son las prensas de neumáticos, planchas de lavandería, vulcanizadoras y autoclaves.
En algunas aplicaciones estáticas, el tiempo de calentamiento del proceso no es importante. Sin embargo, en otros, como tanques y vulcanizadoras, no sólo puede ser importante, si no crucial para el proceso global.
Consideremos dos procesos de calentamiento estáticas que requieran la misma cantidad de energía térmica, pero diferentes tiempos para calentar. Las tasas de transferencia de calor serían diferentes, mientras que la cantidad de calor total transferido sería la misma. La tasa media de transferencia de calor para estas aplicaciones es la siguiente:
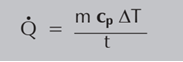
Donde:
Q = Cantidad de energía (kJ)
m = Masa de la sustancia (kg)
cp = Calor específico de la sustancia (kJ/kg °C)
△T = Salto de temperatura de la sustancia (°C)
t = Tiempo del proceso de calentamiento (segundos)
La ecuación anterior se puede aplicar si la sustancia que se calienta es un sólido, un líquido o un gas. Sin embargo, no tiene en cuenta la transferencia de calor implicada cuando se produce un cambio de fase. La cantidad de calor proporcionado por la condensación del vapor se puede determinar con la ecuación siguiente:
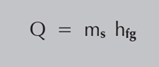
Donde:
Q = Cantidad de energía (kJ)
ms = Masa de la sustancia (kg)
hfg = Entalpía específica de vaporación del agua (kJ/kg)
De ello se desprende que el consumo de vapor se puede determinar a partir de la tasa de transferencia de calor y viceversa, usando la Ecuación:
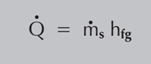
Dónde:
Q = Tasa media de transferencia de calor (kW o kJ/s)
ms = Consumo medio de vapor (kg/s)
hfg = Entalpía específica de evaporación del agua (kJ/kg)
Si se supone en esta etapa que la transferencia de calor tiene una eficiencia del 100%, entonces, el calor proporcionado por el vapor debe ser igual a la demanda de calor del fluido a calentar.
Esto se puede utilizar para crear un equilibrio de calor, en el que la energía térmica suministrada y requerida se equiparan:
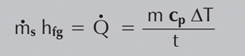
Dónde:
ms = Tasa media de consumo de vapor (kg/s)
hfg = Entalpía específica de evaporación del agua (kJ/kg)
Q = Tasa media de transferencia de calor (kW o kJ/s)
m = Masa del fluido secundario (kg)
cp = Calor específico del fluido secundario (kJ/kg°C)
△T = Salto de temperatura del fluido del secundario (°C)
t = Tiempo del proceso de calentamiento (segundos)
Aplicaciones dinámicas
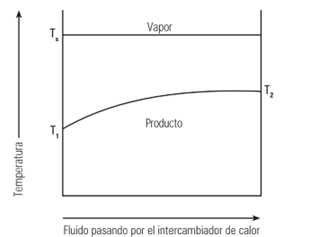
Ejemplos típicos incluyen intercambiadores de calor de tubos, también conocidos como acumuladores sin almacenamiento e intercambiadores de calor de placas, que suministran agua caliente a sistemas de calentamiento o procesos industriales. Otro ejemplo sería una batería calefactora de aire, donde el vapor cede su calor al aire que pasando constantemente.
La Figura siguiente nos muestra un perfil típico de temperatura en un intercambiador de calor con un caudal constante de fluido secundario. La temperatura de condensación (TS) permanece constante en todo el intercambiador de calor. El fluido se calienta desde T1 en la válvula de entrada hasta T2 en la salida del intercambiador de calor.
Para un caudal del secundario fijo, la carga de calor necesaria (Q) es proporcional a la elevación de la temperatura del producto (△T).Utilizando la Ecuación siguiente:
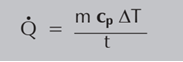
Al ser el caudal del producto y el calor específico constantes y si se asume que el caudal básico es la relación m/t, la ecuación queda de la siguiente manera:

Donde:
Q = Tasa media de transferencia de calor (kW)
m = Caudal medio del fluido secundario (kg/s)
cp = Calor específico del fluido secundario (kJ/kg K) o (kJ/kg°C)
△T = Salto de temperatura del fluido del secundario (K o °C)
Se puede hacer una ecuación de equilibrio de calor para aplicaciones con caudal dinámico donde existe un flujo continuo de fluido:
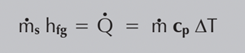
ms = Tasa media de consumo de vapor (kg/s)
hfg = Entalpía específica de evaporación del agua (kJ/kg)
Q = Tasa media de transferencia de calor (kW o kJ/s)
m = Caudal másico del fluido secundario (kg/s)
cp = Calor específico del fluido secundario (kJ/kg°C)
△T = Salto de temperatura del fluido del secundario (°C)
Parámetros de calentamiento y de pérdida de calor
En cualquier proceso de calentamiento, el calor aportado al sistema disminuirá a medida que se eleva la temperatura del producto y se reduce el diferencial de temperatura a través del serpentín de calentamiento. Sin embargo, el parámetro de la pérdida de calor aumentará a medida que aumenta la temperatura del recipiente del producto, ya que se pierde más calor al medio ambiente desde el recipiente o tubería. La demanda total de calor siempre debe tener en cuenta estos dos parámetros.
Si la superficie de calentamiento está calculada sólo considerando el parámetro de calentamiento, es posible que no haya suficiente calor disponible para el proceso para que alcance la temperatura esperada. Cuando se dimensiona el equipo de calentamiento, si se toman en cuenta los valores medios de estos dos parámetros, normalmente debe ser capaz de satisfacer la demanda total de calor de la aplicación.
A veces, en grandes tanques de almacenamiento de petróleo, por ejemplo, puede que sea conveniente mantener una temperatura de conservación inferior a la temperatura requerida de bombeo, de esta manera se reducirán las pérdidas de calor en la superficie del tanque. Se puede emplear otro método de calentamiento, como un intercambiador en la salida.
Los elementos de calentamiento están revestidos con una carcasa metálica introducida en el tanque y diseñada de tal manera que sólo se entrará el petróleo que la rodea y se calentará a la temperatura de bombeo. Por lo tanto sólo precisa calor cuando se extrae el petróleo y, puesto que la temperatura del tanque se reduce, generalmente se puede prescindir del calorifugado. El tamaño de la salida del intercambiador dependerá de la temperatura del petróleo, la temperatura de bombeo y el régimen de bombeo.
Añadir materiales a los tanques de proceso abiertos (atmosféricos) también puede ser considerado como un parámetro de pérdida de calor que aumentará la demanda térmica.
Estos materiales actúan como un disipador de calor cuando se sumergen y hay que tomarlos en cuenta al dimensionar la superficie de calentamiento.
Sea cual sea la aplicación, cuando se tiene que calcular la superficie de transferencia de calor, primero hay que evaluar la tasa media del total de transferencia de calor. Con esto, se podrá determinar la demanda de calor y la carga de vapor, para plena carga y puesta en marcha. Esto permitirá que el tamaño de la válvula de control se base en cualquiera de estas dos condiciones, dependiendo de la elección.



 ¿Qué es el vapor sobrecalentado y cuáles son sus usos en la industria?
¿Qué es el vapor sobrecalentado y cuáles son sus usos en la industria?
Deja una respuesta