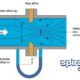
¿Cómo cuantificar la relación entre la caída de presión de vapor y el caudal? Consideremos la analogía de un tanque lleno hasta un determinado nivel con agua y un agujero en el lado del tanque en algún lugar cerca de la parte inferior que, inicialmente, está taponado para evitar que el agua salga, tal y como presentamos en la siguiente figura:

Ahora, consideremos una sola molécula de agua en la parte superior del tanque (molécula 1) y una sola molécula en la parte inferior al mismo nivel que el orificio (molécula 2). Con el agujero taponado, la altura de agua por encima del orificio crea un potencial que fuerza a las moléculas directamente debajo de la molécula 1 a través del agujero.
La energía potencial de la molécula 1 en relación con la molécula 2 dependerá de la altura de la molécula 1 por encima de la molécula 2, la masa de la molécula 1 y el efecto que tiene la fuerza de gravedad sobre la masa de la molécula 1. La energía potencial de todas las moléculas de agua que se encuentran entre la molécula 1 y la molécula 2 se calcula usando la siguiente ecuación:

La molécula 1 no tiene ninguna energía de presión (el efecto neto de la presión del aire es cero, debido a que el tapón en la parte inferior del tanque está sometido también a la misma presión), ni energía cinética (ya que el fluido donde está no está en movimiento). La única energía que posee en relación con el agujero en el tanque es la energía potencial.
Mientras tanto, en la posición opuesta del agujero, la molécula 2 tiene una energía potencial de cero ya que no tiene altura en relación con el agujero. Sin embargo, la presión en cualquier punto en un fluido debe equilibrar el peso de todo el líquido que tiene por encima, además de cualquier fuerza vertical adicional que actúa sobre el punto en consideración. En este caso, la fuerza adicional se debe a la presión atmosférica del aire por encima de la superficie del agua, que se puede considerar como un presión manométrica (relativa) de cero. La presión a la que está sometida la molécula 2 está, por lo tanto, puramente relacionada con el peso de las moléculas que tiene por encima de ella.
El peso es en realidad una fuerza aplicada a una masa debido al efecto de la gravedad y se define como masa x aceleración. El peso que está soportado la molécula 2 es la masa de agua (m) en una línea de moléculas directamente encima, multiplicada por la constante de aceleración de la gravedad, (g). Por lo tanto, la molécula 2 está sometida una fuerza de presión m g.
Pero, ¿Qué energía está contenida en la molécula 2? Como se dijo antes, no tiene energía potencial; tampoco tiene energía cinética, al igual que la molécula 1, no está en movimiento. Por lo tanto solo puede poseer energía de presión.
h = altura acumulativa de moléculas por encima del agujero
Por lo tanto, puede verse que: La energía potencial de la molécula 1 = m g h = Energía de presión en la molécula 2. Esto concuerda con el principio de conservación de la energía (que está relacionado con la Primera Ley de Termodinámica), que establece que la energía no se crea ni se destruye, pero se puede transformar de una forma a otra. En esencia, esto significa que la pérdida de energía potencial significa una ganancia igual en energía de presión.
Consideremos ahora, que se quita el tapón del agujero, como se muestra en la siguiente figura:

Parece intuitivo que el agua salga por el agujero debido a la altura de agua en el tanque. De hecho, la velocidad a la que el agua fluirá a través del agujero está relacionada con la diferencia en energía de presión entre las moléculas de agua opuestas al orificio, en el interior e inmediatamente en el exterior del tanque.
Como la presión en el exterior del tanque es la atmosférica, la energía de presión en cualquier punto fuera del agujero se puede considerar como cero (de la misma forma que la presión aplicada a la molécula 1 era cero). Por lo tanto, la diferencia en energía de presión a través del agujero se puede considerar como la energía de presión contenida en la molécula 2, y por lo tanto, la velocidad a la que el agua fluirá a través del agujero está relacionada con la energía de presión de la molécula 2.
En la figura anterior, consideremos la molécula 2 con una energía de presión de m g h, y consideremos la molécula 3 que acaba de pasar a través del agujero en el tanque, y está contenida en el chorro de agua que sale.
La molécula 3 no tiene ninguna energía de presión por las razones descritas anteriormente, ni energía potencial (ya que el fluido en el que se encuentra está a la misma altura que el agujero). La única energía que tiene sólo puede ser energía cinética.
En algún punto en el chorro de agua inmediatamente después de pasar a través del agujero, la molécula 3 se encuentra en el chorro y tendrá una determinada velocidad y por tanto una determinada energía cinética. Dado que la energía no se puede crear, se deduce que la energía cinética en la molécula 3 se forma a partir de la energía de presión contenida en la molécula 2 inmediatamente antes de que se retirase el tapón del agujero.
Por lo tanto, podemos concluir que la totalidad de la energía cinética contenida en la molécula 3 es igual a la energía de presión a que está sometida la molécula 2, que, a su vez, es igual a la energía potencial contenida en la molécula 1.
La ecuación básica para la energía cinética se muestra en la siguiente ecuación:


Esta ecuación muestra que la velocidad del agua que pasa a través del agujero es proporcional a la raíz cuadrada de la altura del agua o carga de presión (h) por encima del punto de referencia, (el agujero). La altura “h” puede considerarse como una diferencia de presión, también llamada como caída de presión de vapor o “presión diferencial”.
De igual manera, el mismo concepto se aplica a un fluido que pasa a través de un orificio que se ha colocado en una tubería. Un método sencillo de medición de caudal de un fluido es mediante la introducción de un medidor de caudal de placa de orificio en una tubería, creando de ese modo una caída de presión de vapor respecto al fluido que fluye. Midiendo la presión diferencial y aplicando el factor de la raíz cuadrada necesario, se puede determinar la velocidad del fluido que pasa a través del orificio.
El gráfico siguiente, se muestra cómo cambia el caudal en relación a la caída de presión de vapor a través de un medidor de caudal de placa orificio. Podemos ver que, con una caída de presión de vapor de 25 kPa, el caudal es la raíz cuadrada de 25, que son 5 unidades. De la misma manera, el caudal con una caída de presión de vapor de 16 kPa es de 4 unidades, a 9 kPa son 3 unidades y así sucesivamente.

Conociendo la velocidad a través del orificio no sirve de mucho. El objetivo principal de cualquier medidor de caudal es medir el caudal en términos de volumen o masa. Sin embargo, si se conoce el tamaño del agujero, se puede calcular el caudal volumétrico multiplicando la velocidad por el área del agujero. Sin embargo, esto no es tan sencillo como parece a primera vista.
Es un fenómeno de cualquier orificio instalado en una tubería que el fluido, después de pasar a través del orificio, seguirá contrayéndose, debido principalmente al impulso del propio fluido. Esto significa realmente que el fluido pasa a través de una apertura más estrecha que el orificio. A esta apertura se llama “vena contracta” y representa esa parte en el sistema de máxima constricción, mínima presión y máxima velocidad del fluido.
El área de la vena contracta depende de la forma física del agujero, pero se puede predecir para placas orificios estándar de aristas vivas utilizados para estos propósitos. La relación entre la superficie de la vena contracta y la zona del orificio es de aproximadamente 0,65 a 0,7 y, en consecuencia, si se conoce el área del orificio, se puede establecer el área de la vena contracta.
Finalmente, te invitamos a conocer el Teorema de Bernoulli aplicado en caudalímetros de vapor, así como también los principios básicos y terminología de la medición de caudal en sistemas de vapor. Adicionalmente, suscríbete al Newsletter de Vapor para La Industria, un recurso que te servirá para recibir más contenido sobre las nuevas tendencias del vapor industrial, como los regímenes de flujo en mediciones de caudal de vapor.



 Teorema de Bernoulli aplicado en caudalímetros de vapor
Teorema de Bernoulli aplicado en caudalímetros de vapor