A concepção óptima de um sistema de vapor dependerá, em grande medida, de a taxa de consumo de vapor ter sido calculada com precisão. Isto permitirá o dimensionamento das tubagens e o dimensionamento do equipamento auxiliar, tais como válvulas de controlo e purgadores, para proporcionar os melhores resultados possíveis. É possível calcular a procura de vapor da planta, utilizando métodos diferentes:
- CáCálculo - Analisando a produção de calor num elemento vegetal utilizando as equações de transferência de calor, é possível obter uma estimativa do consumo de vapor. Embora a transferência de calor não seja uma ciência exacta e possa haver muitas variáveis desconhecidas, podem ser utilizados dados experimentais anteriores de aplicações semelhantes. Os resultados obtidos com este método são geralmente suficientemente precisos para a maioria dos fins.
- Medición - O consumo de vapor pode ser determinado por medição directa, utilizando equipamento de medição de caudal. Estes fornecem dados relativamente precisos sobre o consumo de vapor de uma instalação existente; contudo, para uma instalação ainda em fase de concepção, ou que ainda não esteja em funcionamento, este método é de pouca utilidade.
- Poder do chármica - A classificação do design é frequentemente dada na placa de identificação de uma peça individual de equipamento numa fábrica, tal como especificado pelo fabricante. Normalmente indica a saída de calor pretendida em kW, mas o consumo de vapor necessário em kg/h dependerá da pressão de vapor recomendada.
Qualquer alteração num parâmetro pode alterar a saída de calor pretendida, o que significa que a saída térmica (concepção) e a carga conectada (consumo real de vapor) não será a mesma. O valor dado pelo fabricante é uma indicação da capacidade ideal de um equipamento e não corresponde necessariamente à carga conectada.
Cálculo do consumo de vapor industrial
Na maioria dos casos, o calor no vapor é necessário para fazer duas coisas:
- Produzir uma mudança na temperatura do produto, fornecendo uma 'componente de aquecimento'.
- Manter a temperatura do produto à medida que se perde calor por causas naturais ou por concepção, fornecendo um componente de "perda de calor".
Em qualquer processo de aquecimento, a 'componente de aquecimento' diminuirá à medida que a temperatura do produto aumenta e o diferencial de temperatura entre a serpentina de aquecimento e o produto é reduzido. No entanto, a componente de perda de calor aumentará à medida que a temperatura do produto aumenta e mais calor é perdido para o ambiente a partir do recipiente ou tubo.
A procura total de calor em qualquer momento é a soma destes dois componentes.
A equação utilizada para estabelecer a quantidade de calor necessária para elevar a temperatura de uma substância pode ser desenvolvida para ser aplicada a uma vasta gama de processos de transferência de calor.
Onde:
Q = Quantidade de energia (kJ)
m = Massa de substância (kg)
cp = Calor específico da substância (kJ/kg °C)
△T = Salto de temperatura da substância (°C)
Na sua forma original, esta equação pode ser utilizada para determinar a quantidade total de energia térmica em todo o processo. No entanto, na sua forma actual, não tem em conta a taxa de transferência de calor. Para estabelecer as taxas de transferência de calor, os diferentes tipos de aplicação de troca de calor podem ser divididos em duas grandes categorias:
- As aplicações sãoPolíticas - em que o produto a ser aquecido é uma massa fixa e um único lote dentro dos limites de um recipiente.
- Aplicações dinâmicasmicas - onde um fluido aquecido flui constantemente sobre a superfície de transferência de calor.
Aplicações estáticas para o cálculo do consumo de vapor
Em aplicações estáticas, o fluido do processo é mantido como um único lote dentro de um recipiente. Uma serpentina de vapor localizada no recipiente, ou uma camisa de vapor em redor do recipiente, constitui a superfície de aquecimento. Exemplos típicos incluem acumuladores de armazenamento de água quente e tanques de armazenamento de óleo, onde um grande tanque circular de aço é enchido com óleo viscoso que requer calor antes de poder ser bombeado.
Alguns processos envolvem o aquecimento de sólidos; exemplos típicos são prensas de pneus, pratos de roupa, vulcanizadores e autoclaves.
Em algumas aplicações estáticas, o tempo de aquecimento do processo não é importante. Contudo, em outras, tais como tanques e vulcanizadores, pode não só ser importante, mas crucial para o processo global.
Considere dois processos de aquecimento estático que requerem a mesma quantidade de energia térmica, mas tempos diferentes para aquecer. As taxas de transferência de calor seriam diferentes, enquanto que a quantidade total de calor transferida seria a mesma. A taxa média de transferência de calor para estas aplicações é a seguinte:
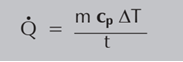
Onde:
Q = Quantidade de energia (kJ)
m = Massa de substância (kg)
cp = Calor específico da substância (kJ/kg °C)
△T = Salto de temperatura da substância (°C)
t = Tempo do processo de aquecimento (segundos)
A equação acima pode ser aplicada quer a substância a ser aquecida seja um sólido, um líquido ou um gás. No entanto, não tem em conta a transferência de calor envolvida quando ocorre uma mudança de fase. A quantidade de calor fornecida pela condensação de vapor pode ser determinada com a seguinte equação:
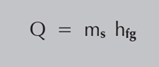
Onde:
Q = Quantidade de energia (kJ)
ms = Massa da substância (kg)
hfg = Enthalpy específico de Vaporização da água (kJ/kg)
Segue-se que o consumo de vapor pode ser determinado a partir da taxa de transferência de calor e vice-versa, usando Eq:
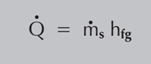
Onde:
Q = Taxa média de transferência de calor (kW ou kJ/s)
ms = Consumo médio de vapor (kg/s)
hfg = Entalpia de evaporação específica da água (kJ/kg)
Se nesta fase se assumir que a transferência de calor tem uma eficiência de 100%, então o calor fornecido pelo vapor deve ser igual à procura de calor do fluido a ser aquecido.
Isto pode ser utilizado para criar um balanço de calor, no qual a energia térmica fornecida e necessária é igualizada:
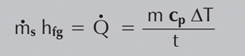
Onde:
ms = Taxa média de consumo de vapor (kg/s)
hfg = Entalpia de evaporação específica da água (kJ/kg)
Q = Taxa média de transferência de calor (kW ou kJ/s)
m = Massa do fluido secundário (kg)
cp = Calor específico do fluido secundário (kJ/kg°C)
△T = Salto de temperatura do fluido secundário (°C)
t = Tempo do processo de aquecimento (segundos)
Aplicações dinâmicas
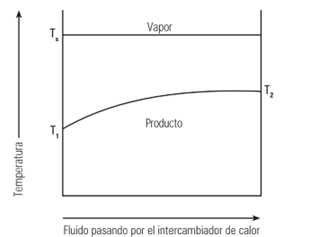
Exemplos típicos incluem permutadores de calor de tubos, também conhecidos como permutadores de calor de armazenamento sem armazenamento e permutadores de calor de placas, que fornecem água quente a sistemas de aquecimento ou processos industriais. Outro exemplo seria uma serpentina de aquecimento de ar, em que o vapor entrega o seu calor ao ar que passa constantemente.
A figura abaixo mostra um perfil típico de temperatura num permutador de calor com um fluxo de fluido secundário constante. A temperatura de condensação (TS) permanece constante em todo o permutador de calor. O fluido é aquecido desde T1 na válvula de entrada até T2 na saída do permutador de calor.
Para um caudal secundário fixo, a carga térmica necessária (Q) é proporcional ao aumento de temperatura do produto (△T) usando a seguinte equação:
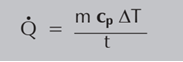
Uma vez que o caudal de produto e o calor específico são constantes e se o caudal de base for assumido como o rácio m/t, a equação é a seguinte:

Onde:
Q = Taxa média de transferência de calor (kW)
m = Caudal médio do fluido secundário (kg/s)
cp = Calor específico do fluido secundário (kJ/kg K) ou (kJ/kg°C)
△T = Aumento da temperatura do fluido secundário (K ou °C)
Uma equação de equilíbrio térmico pode ser feita para aplicações de fluxo dinâmico onde existe um fluxo de fluido contínuo:
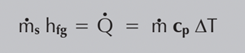
ms = Taxa média de consumo de vapor (kg/s)
hfg = Entalpia de evaporação específica da água (kJ/kg)
Q = Taxa média de transferência de calor (kW ou kJ/s)
m = Caudal de massa do fluido secundário (kg/s)
cp = Calor específico do fluido secundário (kJ/kg°C)
△T = Salto de temperatura do fluido secundário (°C)
Parâmetros de aquecimento e perda de calor
Em qualquer processo de aquecimento, a entrada de calor no sistema irá diminuir à medida que a temperatura do produto aumenta e o diferencial de temperatura através da serpentina de aquecimento diminui. Contudo, o parâmetro de perda de calor aumentará à medida que a temperatura do recipiente do produto aumenta, à medida que mais calor é perdido para o ambiente a partir do recipiente ou tubo. A procura total de calor deve ter sempre em conta estes dois parâmetros.
Se a superfície de aquecimento for calculada apenas considerando o parâmetro de aquecimento, pode não haver calor suficiente para que o processo atinja a temperatura esperada. Ao dimensionar o equipamento de aquecimento, se os valores médios destes dois parâmetros forem tidos em conta, este deverá normalmente ser capaz de satisfazer a procura total de calor da aplicação.
Por vezes, em grandes tanques de armazenamento de petróleo, por exemplo, pode ser desejável manter uma temperatura de armazenamento inferior à temperatura de bombagem necessária, reduzindo assim as perdas de calor à superfície do tanque. Outro método de aquecimento, tal como um permutador de calor na saída, pode ser utilizado.
Os elementos de aquecimento são revestidos com um invólucro metálico inserido no tanque e concebidos de tal forma que apenas o óleo que o envolve entrará e aquecerá até à temperatura de bombagem. Assim, só necessita de calor quando o óleo é extraído e, como a temperatura do tanque é reduzida, é geralmente possível prescindir da califugação. O tamanho da saída do permutador de calor dependerá da temperatura do óleo, da temperatura de bombeamento e da taxa de bombeamento.
A adição de materiais a tanques de processo abertos (atmosféricos) também pode ser considerada como um parâmetro de perda de calor que irá aumentar a procura térmica.
Estes materiais actuam como dissipadores de calor quando submersos e devem ser tidos em conta ao dimensionar a superfície de aquecimento.
Qualquer que seja a aplicação, quando a superfície de transferência de calor tem de ser calculada, a taxa média da transferência total de calor deve ser avaliada primeiro. Com isto, é possível determinar a procura de calor e a carga de vapor, para carga total e arranque. Isto permitirá que a válvula de controlo seja dimensionada com base numa destas duas condições, dependendo da escolha.



 O que é vapor sobreaquecido e quais são as suas utilizações na indústria?
O que é vapor sobreaquecido e quais são as suas utilizações na indústria?
Deixe uma resposta