Queda de pressão de vapor e sua relação com a vazão: como quantificá-la?

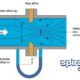
Como quantificar a relação entre a queda de pressão de vapor e a vazão? Considere a analogia de um tanque cheio até um certo nível com água e um buraco na lateral do tanque em algum lugar perto do fundo que está inicialmente tapado para evitar a fuga de água, como mostrado na figura abaixo:

Agora, considere uma única molécula de água na parte superior do tanque (molécula 1) e uma única molécula na parte inferior no mesmo nível do buraco (molécula 2). Com o buraco tapado, a altura da água acima do buraco cria um potencial que força as moléculas diretamente abaixo da molécula 1 através do buraco.

A energia potencial da molécula 1 em relação à molécula 2 dependerá da altura da molécula 1 acima da molécula 2, da massa da molécula 1 e do efeito que a força da gravidade tem sobre a massa da molécula 1. A energia potencial de todas as moléculas de água entre a molécula 1 e a molécula 2 é calculada usando a seguinte equação:

A molécula 1 não tem energia de pressão (o efeito líquido da pressão do ar é zero, porque o obturador no fundo do tanque também está sob a mesma pressão), nem energia cinética (uma vez que o fluido em que se encontra não está em movimento). A única energia que possui em relação ao buraco no tanque é a energia potencial. 

Entretanto, na posição oposta do buraco, a molécula 2 tem uma energia potencial de zero, uma vez que não tem altura em relação ao buraco. No entanto, a pressão em qualquer ponto de um fluido deve equilibrar o peso de todo o líquido acima dele, mais quaisquer forças verticais adicionais atuando no ponto em consideração. Neste caso, a força adicional é devida à pressão atmosférica do ar acima da superfície da água, que pode ser considerada como uma pressão manométrica (relativa) de zero. A pressão a que a molécula 2 é submetida está, portanto, puramente relacionada com o peso das moléculas acima dela. 

O peso é na verdade uma força aplicada a uma massa devido ao efeito da gravidade e é definido como massa x aceleração. O peso suportado pela molécula 2 é a massa de água (m) em uma linha de moléculas diretamente acima dela, multiplicada pela constante de aceleração da gravidade, (g). Portanto, a molécula 2 é submetida a uma força de pressão m g. 

Mas que energia está contida na molécula 2? Como dito anteriormente, não tem energia potencial; também não tem energia cinética, assim como a molécula 1, não está em movimento. Portanto, só pode possuir energia de pressão. 

Portanto, isso pode ser visto: Energia potencial da molécula 1 = m g h = Energia de pressão na molécula 2. Isto concorda com o princípio da conservação da energia (que está relacionado com a Primeira Lei da Termodinâmica), que afirma que a energia não é criada nem destruída, mas pode ser transformada de uma forma para outra. Em essência, isto significa que a perda de energia potencial significa um ganho igual em energia de pressão. 

Considere agora, que a ficha é removida do buraco, como mostra a figura seguinte:

Parece intuitivo que a água sairá do buraco por causa da altura da água no tanque. Na verdade, o ritmo a que a água irá fluir através do buraco está relacionado com a diferença de energia de pressão entre as moléculas de água opostas ao buraco, dentro e imediatamente fora do tanque.

Como a pressão fora do tanque é atmosférica, a energia de pressão em qualquer ponto fora do buraco pode ser considerada zero (tal como a pressão aplicada à molécula 1 foi zero). Portanto, a diferença de energia de pressão através do buraco pode ser considerada como a energia de pressão contida na molécula 2 e, portanto, a taxa a que a água fluirá através do buraco está relacionada com a energia de pressão da molécula 2.

Na figura acima, considere a molécula 2 com uma energia de pressão de m g h, e considere a molécula 3 que acabou de passar pelo buraco no tanque, e que está contida no jato de água que sai.

A molécula 3 não tem energia de pressão pelas razões descritas acima, nem energia potencial (uma vez que o fluido em que se encontra está à mesma altura que o buraco). A única energia que ela tem só pode ser energia cinética. 

Em algum ponto do fluxo de água imediatamente após passar pelo buraco, a molécula 3 está no fluxo e terá uma certa velocidade e, portanto, uma certa energia cinética. Como a energia não pode ser criada, segue-se que a energia cinética na molécula 3 é formada a partir da energia de pressão contida na molécula 2 imediatamente antes de o tampão ser removido do orifício. 

Portanto, podemos concluir que a energia cinética total contida na molécula 3 é igual à energia de pressão da molécula 2, que por sua vez é igual à energia potencial contida na molécula 1. 

A equação básica para a energia cinética é mostrada na seguinte equação:

Esta equação mostra que a velocidade da água que passa através do buraco é proporcional à raiz quadrada da altura da água ou da carga de pressão (h) acima do ponto de referência, (o buraco). A altura "h" pode ser considerada como uma diferença de pressão, também chamada de queda de pressão de vapor ou "pressão diferencial". 

Da mesma forma, o mesmo conceito se aplica a um fluido que passa por um orifício que foi colocado em um tubo. Um método simples de medição do caudal de um fluido é a inserção de um caudalímetro de placa de orifício numa tubagem, criando assim uma queda de pressão de vapor em relação ao fluido que flui. Medindo a pressão diferencial e aplicando o fator raiz quadrada necessária, a velocidade do fluido que passa pelo orifício pode ser determinada. 

O gráfico abaixo mostra como a vazão muda em relação à queda de pressão de vapor através de um medidor de vazão de placa de orifício. Podemos ver que, com uma queda de pressão de vapor de 25 kPa, o caudal é a raiz quadrada de 25, que é de 5 unidades. Da mesma forma, o caudal a uma queda de pressão de vapor de 16 kPa é de 4 unidades, a 9 kPa é de 3 unidades e assim sucessivamente. 

Conhecer a velocidade através do orifício é de pouca utilidade. O principal objectivo de qualquer medidor de caudal é medir o caudal em termos de volume ou massa. No entanto, se o tamanho do orifício for conhecido, o fluxo volumétrico pode ser calculado multiplicando a velocidade pela área do orifício. No entanto, isto não é tão simples como pode parecer à primeira vista. 

É um fenómeno de qualquer orifício instalado num tubo que o fluido, depois de passar pelo orifício, continuará a contrair-se, principalmente devido ao impulso do próprio fluido. Isto significa que o fluido passa por uma abertura que é mais estreita que o orifício. Esta abertura é chamada de "vena contracta" e representa aquela parte do sistema de constrição máxima, pressão mínima e velocidade máxima do fluido.

A área da contracta da veia depende da forma física do furo, mas pode ser prevista para placas de furos afiados padrão utilizadas para estes fins. A razão entre a área da contracta da veia e a área do buraco é de aproximadamente 0,65 a 0,7 e, consequentemente, se a área do buraco for conhecida, a área da contracta da veia pode ser estabelecida.

Finalmente, convidamo-lo a conhecer o O teorema de Bernoulli aplicado aos caudalímetros de vaporbem como a princípios básicos e terminologia da medição de vazão em sistemas de vapor. Além disso, subscreva o Boletim Informativo Steam for IndustryO novo recurso de vapor industrial, um recurso que o ajudará a receber mais conteúdo sobre as novas tendências do vapor industrial, tais como o regimes de vazão em medições de vazão de vapor.